Олимпиадная задача по планиметрии: отношение отрезков в трапеции для 7-9 классов
Задача
В трапеции ABCD основание AD в четыре раза больше чем BC. Прямая, проходящая через середину диагонали BD и параллельная AB, пересекает сторону CD в точке K. Найдите отношение DK : KC.
Решение
Пусть P – середина BD, L и N – точки пересечения прямой KP с прямыми BC и AD соответственно (см. рис.).
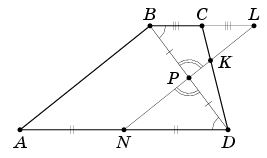
Ответ
DK : KC = 2 : 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет