Олимпиадная задача по стереометрии: площадь треугольника на сфере (10–11 класс)
Задача
В пространстве заданы три луча: DA, DB и DC,
имеющие общее начало D, причём ∠ADB = ∠ADC = ∠BDC = 90°.
Сфера пересекает луч DA в точках A1 и A2, луч
DB – в точках B1 и B2, луч DC
– в точках C1 и C2.
Найдите площадь треугольника A2B2C2,
если площади треугольников DA1B1,
DA1C1, DB1C1 и
DA2B2 равны соответственно
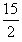, 10, 6 и 40.
Решение
Докажем сначала следующее утверждение: если рёбра треугольной пирамиды попарно перпендикулярны,
то квадрат площади основания равен сумме квадратов площадей боковых граней.Действительно, пусть OX, OY и OZ – попарно перпендикулярные
боковые рёбра треугольной пирамиды OXYZ с вершиной O (рис.1), причём
,
,
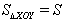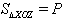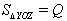. Обозначим
OX = a, OY = b, OZ = c. Тогда 
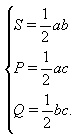перемножив почленно два первых уравнения системы и разделив результат на третье, получим, что
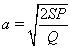.Пусть 
.
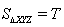Докажем, что T2 = S2 + P2 + Q2.
Для этого опустим перпендикуляр OF из вершины O на ребро YZ.
Ребро OX перпендикулярно плоскости грани OYZ, так как OX ⊥ OY
и OX ⊥ OZ по условию задачи. Тогда прямая YZ
перпендикулярна плоскости OXF, значит XF ⊥ YZ,
т.е. XF – высота треугольника XYZ. Из прямоугольных треугольников
YOZ и XOF находим, что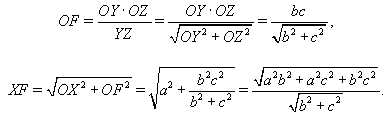 
Значит, 
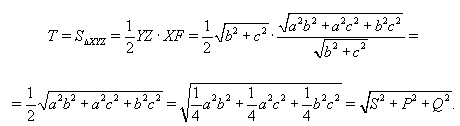Следовательно, T2 = S2 +
P2 + Q2. Что и требовалось доказать.Перейдём к нашей задаче (рис.2). Проведём сечение сферы плоскостью
DA1B1. Получим окружность и две
секущие DA1A2 и DB1B2,
проведённые к ней из точки D, лежащей вне окружности. Тогда DA1·
DA2 = DB1·DB2. Аналогично докажем, что
DA1·DA2 = DC1·DC2.
Кроме того,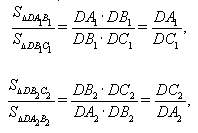 
значит, 
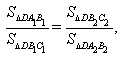откуда 
Аналогично,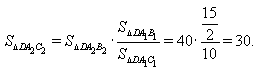 
Следовательно,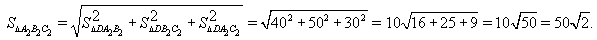 
Ответ
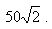
Чтобы оставлять комментарии, войдите или зарегистрируйтесь