Олимпиадная задача о трапеции и окружности: доказательство равенства углов, 8-10 класс
Задача
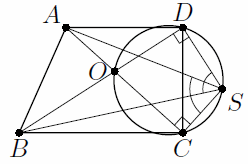
В трапеции ABCD боковая сторона CD перпендикулярна основаниям, O – точка пересечения диагоналей. На описанной окружности треугольника OCD взята точка S, диаметрально противоположная точке O. Докажите, что ∠BSC = ∠ASD.
Решение
Так как SO – диаметр, то ∠SCA = ∠SCO = ∠SDO = ∠SDB = 90°. Из прямоугольных треугольников ADC и BCD
AC : BD = cos∠BDC : cos∠ACD = cos∠ODC : cos∠OCD = sin∠SDC : sin∠SCD = SC : SD (последнее равенство следует из теоремы синусов). Следовательно, прямоугольные треугольники SCA и SDB подобны. Поэтому углы BSC и ASD равны, как дополняющие равные углы BSD и ASC до угла CSD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет