Олимпиадная задача по планиметрии и стереометрии от Агаханова — доказательство параллелограмма в пирамиде
Задача
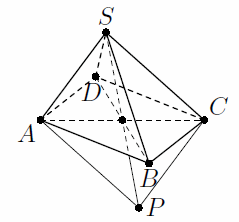
Через вершины основания четырёхугольной пирамиды SABCD проведены прямые, параллельные противоположным боковым рёбрам (через вершину A – параллельно SC, и так далее). Эти четыре прямые пересеклись в одной точке. Докажите, что четырёхугольник ABCD – параллелограмм.
Решение
Пусть P – точка пересечения данных прямых. Поскольку PA || SC и PC || SA, четырёхугольник ASCP – параллелограмм. Значит, прямая SP делит отрезок AC пополам. Аналогично, прямая SP делит отрезок BD пополам. Следовательно, прямая SP пересекает плоскость основания пирамиды в точке пересечения диагоналей четырёхугольника ABCD, и диагонали делятся этой точкой пополам. Поэтому ABCD – параллелограмм.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет