Олимпиадная задача по планиметрии и комбинаторной геометрии: диагонали 2011-угольника

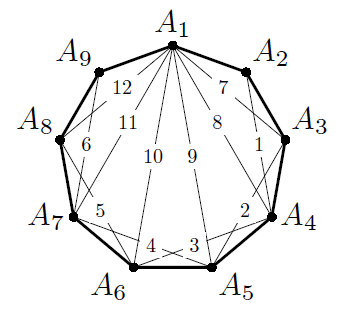
  Докажем, что в выпуклом n-угольнике A₁A₂...A_n максимальное количество диагоналей, которое можно провести указанным способом, равно  2n – 6.  Петя может провести последовательно диагонали  A₂A₄, A₃A₅, A₄A₆, ..., A_n–2A_n,  а затем – диагонали  A₁A₃, A₁A₄, A₁A₅, ..., A₁A_n–1;  итого  2n – 6  диагоналей. На рисунке приведён пример для  n = 9.

  Шаг индукции. Пусть для определённости A₁A_k – последняя проведённая диагональ. Она пересекает не более, чем одну проведённую ранее диагональ (обозначим её d, если она существует).

  Все диагонали, кроме A₁A_k и, возможно, d, проводились либо в k-угольнике A₁A₂...A_k, либо в (n+2–k)-угольнике A_kA_k+1...A_nA₁. По предположению индукции, этих диагоналей не больше  (2k – 6) + (2(n + 2 – k) – 6) = 2n – 8.  Учитывая диагонали A₁A_k и d, получаем, что общее количество диагоналей не больше  2n – 6.   Второй способ. Будем красить проводимые диагонали в красный и синий цвета: первую диагональ окрасим синим; далее, если вновь проведённая диагональ пересекает синюю, то окрасим её красным, иначе – синим. Ясно, что одноцветные диагонали не будут пересекаться по внутренним точкам.

  Пусть есть k одноцветных диагоналей. Поскольку они не имеют общих внутренних точек, то разбивают n-угольник на  k + 1  многоугольников. У каждого из них не менее трёх сторон, значит, суммарное количество S их сторон не меньше  3(k + 1).  С другой стороны, стороны этих многоугольников – это наши диагонали (каждая посчитана по два раза) и стороны исходного n-угольника. Значит,  n + 2k = S ≥ 3(k + 1),  или  k ≤ n – 3.  Итак, диагоналей каждого цвета не больше  n – 3,  а всего проведено не более  2(n – 3)  диагоналей.

4016 диагоналей.