Олимпиадная задача по теории чисел: равенство наибольших простых делителей троек

  Пусть p – нечётное простое число, а  a < p  – такое натуральное число, что  a² + 1  кратно p; тогда числа a и  p – a  различны, и  P(a) = P(p – a) = p.  Действительно, числа  a² + 1  и  (p – a)² + 1 = (a² + 1) + p(p – 2a)  делятся на p и меньше p²; значит, они не могут делиться на простые числа, большие p.  Дальше можно рассуждать по-разному.

  Первый способ. Предположим противное. Тогда существует лишь конечное число простых чисел p, для которых уравнение  P(x) = p  имеет хотя бы три натуральных решения. Обозначим через s максимальное такое простое число (если таких простых не существует, положим  s = 2),  а через S – произведение всех простых чисел, не превосходящих s.

  Пусть  p = P(S);  тогда p взаимно просто с S и потому  p > s.  Пусть a – остаток от деления S на p; тогда  a² + 1  кратно p, значит,  P(a) = P(p – a) = p.  Одно из чисел a и  p – a  чётно; обозначим его через b.

  Число  (b + p)² + 1  делится на 2p (b чётно, а p – нет), поэтому  q = P(b + p) ≥ p.

  Если  q = p,  то уравнение  P(x) = p  имеет три решения – b,  p – b,  p + b;  а это невозможно по предположению.

  Если  q > p,  число  (b + p)² + 1 делится на 2pq. Это означает, что  q < b + p  (в противном случае  (b + p)² + 1 ≤ (2p – 1)q + 1 < 2pq).  Обозначая через c остаток от деления числа  b + p  на q, получаем  P(c) = P(q – c) = P(b + p) = q > p > s,  что противоречит выбору s.   Второй способ. Мы будем использовать тождество   (m² + 1)((m – 1)² + 1) = (m² – m + 1)² + 1,   (*).

Из него следует, что  P(m² – m + 1) = max (P(m), P(m – 1)).

  Предположим противное. Пусть N – наибольшее число, встречающееся в описанных тройках; если таких троек нет, положим  N = 3.  Последовательность натуральных чисел  P(N + 1), P(N + 2), ...  не может строго убывать. Значит, найдётся такое число  n > N + 1,  что  P(n – 1) ≤ P(n).  Тогда  P(n² – n + 1) = max (P(n), P(n – 1)) = P(n).  Из чисел  P(n), P(n + 1), ..., P(n² – n)  выберем максимальное – P(m). Имеем

P(m² – m + 1) = max (P(m),  P(m – 1)) = P(m)  и  P(m² + m + 1) = max (P(m),  P(m + 1)) = P(m).

  Таким образом, тройка  m,  m² – m + 1,  m² + m + 1  удовлетворяет условию, и  m > N. Противоречие.   Третий способ. Для каждого натурального  n ≥ 1  рассмотрим число 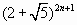  ;   оно имеет вид 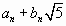   при некоторых натуральных a_n, b_n  (ясно, что  a_n < a_n+1).

  Тогда 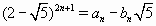 ,  откуда  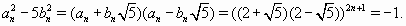   Значит,  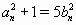 ;   ясно, что  b_n < a_n  и

a_n ≥ 2²ⁿ⁺¹ ≥ 8,  поэтому все простые делители числа 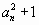   не превосходят  max (5, b_n) < a_n.

  Итак,  p_n = P(a_n) < a_n.  С другой стороны, 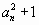   кратно 5, значит,  p_n ≥ 5.  Обозначим через c_n остаток от деления a_n на p_n. Тогда числа c_n,  p_n – c_n  различны и  P(c_n) = P(p_n – c_n) = P(a_n).  Мы предъявили бесконечно много различных троек требуемого вида.

Ответ задачи отсутствует