Олимпиадная задача по планиметрии: точки X на окружности в четырёхугольнике
Задача
Четырёхугольник ABCD без параллельных сторон вписан в окружность. Для каждой пары касающихся окружностей, одна из которых имеет хорду AB, а другая – хорду CD, отметим их точку касания X. Докажите, что все такие точки X лежат на одной окружности.
Решение
Обозначим через Ω1 и Ω2 касающиеся окружности, содержащие соответственно хорды AB и СD, а через Ω – описанную окружность четырёхугольника ABCD. Пусть O – точка пересечения прямых AB и СD. Тогда прямая AB – радикальная ось окружностей Ω1 и Ω (см. задачу 156715), CD – радикальная ось окружностей Ω2 и Ω, а общая касательная окружностей Ω1 и Ω2 – их радикальная ось. Эти три радикальные оси пересекаются в радикальном центре O всех трёх окружностей (см. задачу 161192).
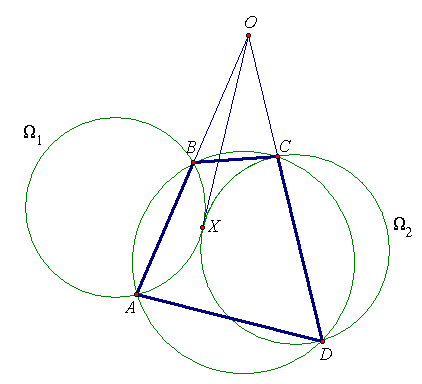
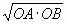с центромO.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь