Олимпиадная задача по комбинаторной геометрии: покрытие плоскости прямоугольниками и квадратами

  а) Построим пример, когда нельзя покрыть даже круг радиуса 1. Сделаем ширину n-го прямоугольника равной 2^–n. Его пересечение с единичным кругом лежит в прямоугольнике 2×2^–n, значит, он покрывает площадь, меньшую 2^–n+1. В совокупности прямоугольники покроют площадь, меньшую 2, что меньше площади круга.   б) Если среди квадратов есть бесконечное число со стороной больше некоторого числа a, то утверждение очевидно. Поэтому далее мы считаем, что для каждого a таких квадратов – конечное число. Это, в частности, означает что квадраты можно упорядочить по убыванию площади. Разобьём плоскость на единичные клетки и занумеруем их по спирали. Заметим, что достаточно покрыть конечным числом данных квадратов одну клетку. Действительно, после этого у нас снова останется бесконечное число квадратов с бесконечной суммарной площадью. Ими можно покрыть следующую клетку, и т. д.

  Дадим два способа покрытия единичной клетки.   Первый способ. Если есть квадрат со стороной не меньше 1, просто накроем им клетку. В противном случае будем располагать квадраты в клетке рядами по убыванию, как на рисунке. Ставим квадраты на основание клетки, следующий вплотную к предыдущему.

  Пусть сумма площадей квадратов превзошла 1. Поскольку площадь каждого квадрата численно меньше длины его стороны, то и сумма сторон будет больше 1, поэтому в какой-то момент все основание клетки будет покрыто, и очередной квадрат со сторонойb₁вылезет, хотя бы частично, за правую сторону клетки. Отрежем полосу высотыb₁. Часть клетки вне полосы будем считать полностью не покрытой и начнём ставить следующий ряд квадратов на верхнюю границу полосы, начиная с её левого конца. Пусть следующая полоса заканчивается квадратом со сторонойb₂и т. д.   Докажем, что сумма высот полос  b₁+b₂+ ...  рано или поздно превзойдёт 1. Ширина каждой полосы не превосходит 2. Высота всех квадратов из (i+1)-й полосы не большеb_i, поэтому сумма их площадей не превышает 2b_i. Выкладываем полосы, пока сумма площадей квадратов во всех законченных полосах, кроме первой, не превзойдёт 2. В этот момент  2b₁+ 2b₂+ ... + 2b_n≥ 2,  откуда  b₁+b₂+ ... +b_n≥ 1.  Это означает, что полосы покрыли клетку целиком. Переходим к следующей клетке...   Второй способ. Пусть  a₁ ≥ a₂ ≥ ...  – размеры квадратов. Разобьём каждый из них на девять равных квадратиков и центральный квадратик окрасим в чёрный цвет. Будем класть квадраты на клетку по порядку, соблюдая следующие условия:

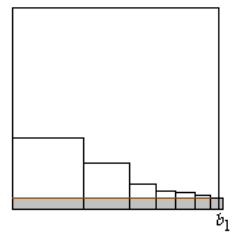
    а) стороны квадратов параллельны сторонам клетки;

    б) чёрные квадратики "задевают" клетку и не пересекаются между собой. Общая сумма площадей чёрных квадратиков также бесконечна, поэтому когда-нибудь процесс прекратится: квадрат со стороной a_n уже нельзя будет уложить с соблюдением условий. Докажем, что в этот момент клетка уже покрыта.

  Пусть A – произвольная точка клетки. Чёрный квадратик со стороной ⅓ a_n и центром A должен пересекаться с одним из ранее уложенных чёрных квадратиков (со стороной  ⅓ a_m ≥ ⅓ a_n).  Поэтому A лежит внутри уже уложенного соответствующего квадрата со стороной a_m.

а) Не обязательно.  б) Обязательно.