Олимпиадная задача по математике: ортоцентр DEH на CP, 10

Задача

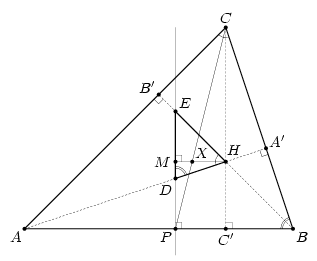
H – точка пересечения высот AA' и BB' остроугольного треугольника ABC. Прямая, перпендикулярная AB, пересекает эти высоты в точках D и E, а сторону AB – в точке P. Докажите, что ортоцентр треугольника DEH лежит на отрезке CP.

Решение

Пусть X – точка пересечения высоты HM треугольника DEH с отрезком CP (см. рис.). Докажем, что X – ортоцентр треугольника DEH.

ТреугольникDEHподобен треугольникуBACпо двум углам. Так как отношение, в котором ортоцентры подобных треугольников разбивают соответствующие высоты одинаково, то достаточно проверить, что HX:XM = CH:HC' (CC'– высота треугольникаABC). Но это равенство следует из равенства отрезковMPиHC'и подобия треугольниковMXPиHXC.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии и стереометрии 10–11 класс: ортоцентр треугольника DEH

Задача

Решение

Ответ

Подтверждение удаления