Олимпиадная задача по математике: пересечения парабол, 10–11 класс, Карасев
Задача
На координатной плоскости нарисовано n парабол, являющихся графиками квадратных трёхчленов; никакие две из них не касаются. Они делят плоскость на несколько областей, одна из которых расположена над всеми параболами. Докажите, что у границы этой области не более 2(n – 1) углов (то есть точек пересечения пары парабол).
Решение
Индукция по n.
База. При n = 1 утверждение очевидно.
Шаг индукции. Пусть f1(x), f2(x), ..., fn(x) – данные квадратные трёхчлены (n ≥ 2), причём fn(x) – трёхчлен с минимальным старшим членом (если таких несколько, то любой из них). Обозначим границу нашей области через T. Можно считать, что T содержит участки всех графиков.
Пусть S – множество всех таких чисел a, что точка множества T с абсциссой a лежит на графике трёхчлена fn(x). Иначе говоря, число a принадлежит
S тогда и только тогда, когда выполнены неравенства fn(x) ≥ fi(a) при всех i = 1, 2, ..., n – 1. Обозначим через Si множество всех решений i-го неравенства; тогда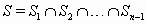 
. Поскольку трёхчлен fn(x) – fi(x) либо обладает отрицательным старшим коэффициентом, либо является на самом деле линейным, Si – это либо отрезок (возможно, вырожденный), либо луч, либо вся прямая. Значит, и S является множеством такого же вида.
Итак, у T не более двух углов, принадлежащих графику fn(x). Если мы удалим этот график, исчезнут эти углы (и, возможно, появятся новые). При этом по предположению индукции новая область будет иметь не более 2(n – 2) углов; значит, исходная имела не более 2(n – 2) + 2 = 2(n – 1) углов.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь