Олимпиадная задача Шаповалова: Сумма по периметру в квадрате 7×7 (текстовая задача для 9-11 класса)
Задача
В каждой клетке клетчатого квадрата 7×7 стоит по числу. Сумма чисел в каждом квадратике 2×2 и 3×3 равна 0.
Докажите, что сумма чисел в 24 клетках, расположенных по периметру квадрата, тоже равна 0.
Решение
Решение 1:Так как равна нулю сумма и в квадратике 3×3, и во входящем него квадрате 2×2, то равна нулю и сумма в остающемся уголке из 5 клеток. По аналогичной причине равна нулю сумма чисел в уголке из 7 клеток, получающемся выкидыванием из квадрата 4×4 (то есть четырёх квадратов 2×2) квадрата 3×3. Осталось заметить, что из уголков двух таких видов можно составить рамку квадрата 7×7 (рис. слева).
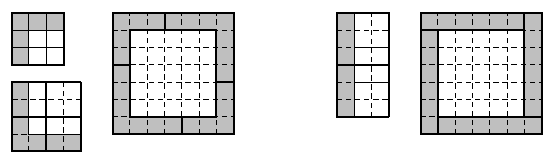
Решение 2:Из двух квадратов 3×3 можно составить прямоугольник 3×6, а из трёх квадратов 2×2 – прямоугольник 2×6. Поэтому сумма чисел в любом прямоугольнике 1×6 равна нулю. Осталось заметить, что из четырёх прямоугольников 1×6 можно составить рамку квадрата 7×7.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь