Назад

Олимпиадная задача по математике: инварианты, алгебра, 6-7 класс, квадрат 3×3

Задача 216845 • Сложность: 2 • 6-7 класс
Задача

В клетках квадрата 3×3 расставлены числа (рис. слева). Разрешается к числам, стоящим в двух соседних клетках, одновременно прибавлять одно и то же число, не обязательно положительное. Можно ли в какой-то момент получить такой квадрат с числами, как на рисунке справа? (Клетки считаются соседними, если имеют общую сторону.)

Разделы:
Инварианты и полуинварианты Вспомогательная раскраска Алгебраические методы
Источники:
Окружная олимпиада (Москва) Олимпиады и турниры 2012 год 7 класс
Количество версий:
4
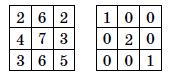
Решение

Раскрасим все клетки в шахматном порядке (см. рисунок).

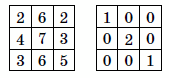
Назовём числабелыми(чёрными), если они стоят на белых (чёрных) клетках. Заметим, что в исходном квадрате сумма белых чисел равна сумме чёрных. Прибавляя к числам, стоящим в соседних клетках, одно и то же число, мы одинаково изменяем сумму белых и сумму чёрных чисел. Поэтому равенство сумм не нарушится. Но во втором квадрате сумма белых чисел равна 0, а сумма чёрных равна 4. Поэтому такой квадрат не может получиться из исходного.
Ответ

Нельзя.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет