Назад

Олимпиадная задача про "супер-слонов" Васи на шахматной доске — текстовые задачи 9-10 класс

Задача 216871 • Сложность: 2 • 9-10 класс
Задача

Вася придумал новую шахматную фигуру "супер-слон". Один "супер-слон" (обозначим его A) бьёт другого (обозначим его B), если они стоят на одной диагонали, между ними нет фигур, и следующая по диагонали клетка за "супер-слоном" B свободна. Например, на рисунке фигура a бьёт фигуру b, но не бьёт ни одну из фигур c, d, e, f и g.

Какое наибольшее количество "супер-слонов" можно поставить на шахматную доску так, чтобы каждый из них бился хотя бы одним другим?
Разделы:
Текстовые задачи Примеры и контрпримеры. Конструкции
Источники:
Окружная олимпиада (Москва) Олимпиады и турниры 2012 год 10 класс
Количество версий:
5
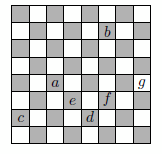
Решение

  Пример приведён на рисунке.

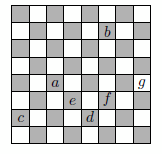
  Оценка. Докажем, что больше 32 фигур разместить не удастся. Заметим сначала, что на крайних клетках доски "супер-слоны" стоять не могут (иначе их никто не бьёт). Разобьём внутренний квадрат 6×6 на четыре квадрата 3×3 (см. рис.). В каждом из этих квадратов все клетки занятыми быть не могут, поскольку в противном случае "супер-слон", стоящий в центральной клетке маленького квадрата, никем не бьётся. Следовательно, можно поставить не более  6·6 – 4 = 32  фигур.
Ответ

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет