Олимпиадная задача по стереометрии: равенство проекций рёбер усечённой пирамиды
Задача
В правильной четырёхугольной усечённой пирамиде середина N ребра B1C1 верхней грани A1B1C1D1 соединена с серединой M ребра AB нижней грани ABCD. Прямые B1C1 и AB не лежат в одной плоскости. Докажите, что проекции рёбер B1C1 и AB на прямую MN равны между собой.
Решение
Утверждение равносильно тому, что равны проекции на прямую MN отрезков MB и B1N (вдвое меньшей длины, см. рисунок), то есть тому, что 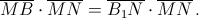
Введём прямоугольную декартову систему координат ОXYZ так, как показано на рисунке (О – центр нижнего основания АВСD, оси x и y параллельны сторонам основания). Пусть длины рёбер большего и меньшего оснований равны 2а и 2b соответственно, а высота пирамиды равна h.

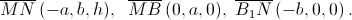 Значит,
Значит, 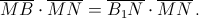
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет