Олимпиадная задача: касательная, биссектрисы и отрезки в треугольнике АВС (Шарыгин, 10-11 класс)
Задача
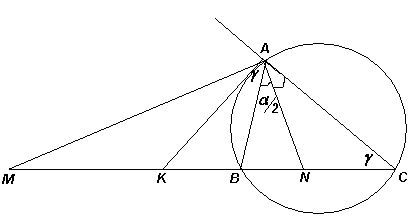
Через вершину А остроугольного треугольника АВС проведены касательная АК к его описанной окружности, а также биссектрисы АN и AM внутреннего и внешнего углов при вершине А (точки М, K и N лежат на прямой ВС). Докажите, что MK = KN.
Решение
Заметим, что ∠MAN = 90°, так как этот угол образован биссектрисами смежных углов (см. рисунок). Обозначим величины углов A и C данного треугольника через α и γ соответственно. Тогда ∠KAB = ∠ACB = γ (угол между касательной и хордой), ∠KNA = α/2 + γ (внешний угол треугольника ACN). Значит, в треугольнике AKN ∠KAN = α/2 + γ = ∠KNA, следовательно, KA = KN. Таким образом, AK – медиана прямоугольного треугольника MАN, проведённая к гипотенузе, то есть K – середина MN.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь