Олимпиадная задача: пересечение шестиугольных сечений в кубе, планиметрия и стереометрия

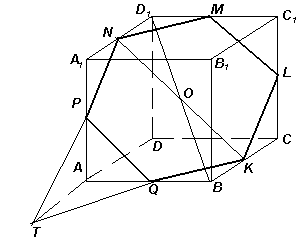
  Пусть PQKLMN – сечение куба ABCDA₁B₁C₁D₁, являющееся правильным шестиугольником (см. рисунок).

  Пусть прямыеPNиKQпересекаются в точкеTна прямойAD. Очевидно, треугольникKTNравнобедренный. Значит,  TP = TQ,  и прямоугольные треугольникиAPTиAQTравны по катету и гипотенузе. Поэтому треугольникPAQ– равнобедренный прямоугольный. То же верно для треугольникаKBQ. Эти треугольники равны по гипотенузе, следовательно,  AQ = BQ.  Аналогично доказывается, что остальныевершины сечениятакже являютсясерединами рёбер куба.  Центр сеченияявляется серединой его диагоналиKN, которая совпадает с серединой диагоналиBD₁куба, то есть сцентром куба.   Заметим, что два сечения, указанных в условии задачи, имеют общий отрезок, соединяющий середины противоположных рёбер куба. Действительно, всего у куба 12 рёбер. Если середины шести из них являются вершинами сечения, то из оставшихся шести точек в одной плоскости лежат не более четырёх. Поэтому два таких сечения имеют две общие вершины, которые лежат на противоположных рёбрах куба. Так как оба сечения симметричны относительно центра куба, то эти вершины лежат на противоположных рёбрах куба. Следовательно, сечения пересекаются по отрезку, соединяющему середины этих рёбер. Длина такого отрезка равна диагонали грани куба, то есть  .