Олимпиадная задача по планиметрии: сумма расстояний от точки до вершин выпуклого четырёхугольника
Задача
Существует ли такие выпуклый четырёхугольник и точка P внутри него, что сумма расстояний от P до вершин больше периметра четырёхугольника?
Решение
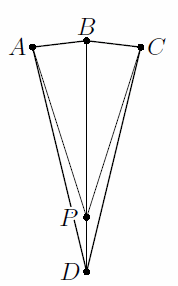
Пусть в четырёхугольнике ABCD AD = BD = CD = x, AB = BC = y < x/4, а P – такая точка на диагонали BD, что PD = y (см. рис.). Тогда
PB + PD = BD = x, PA = PC > AD – PD = x – y, следовательно, PA + PB + PC + PD > 3x – 2y > 2x + 2y = AB + BC + CD + DA.
Ответ
Существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет