Назад

Олимпиадная задача по стереометрии: неравенство для тетраэдра с точкой вне, 9-10 класс

Задача 216916 • Сложность: 2 • 9-10 класс
Задача

Дан тетраэдр ABCD. Точка X выбрана вне тетраэдра так, что отрезок XD пересекает грань ABC во внутренней точке. Обозначим через A', B', C' проекции точки D на плоскости XBC, XCA, XAB соответственно. Докажите, что  A'B' + B'C' + C'A' < DA + DB + DC.

Авторы:
Ясинский В.
Разделы:
Стереометрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
5
Решение

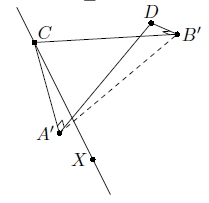
Поскольку  DA' ⊥ (XBC),&nbsp то  ∠DA'C = 90°,  аналогично  ∠DB'C = 90°  (см. рис.). Значит, точки A' и B' лежат на сфере с диаметром DC, поэтому расстояние между ними не превосходит этого диаметра: A'B' < DC. Аналогично  A'C' < DB  и  B'C' < DA.  Складывая эти три неравенства, получаем требуемое.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет