Олимпиадная задача по стереометрии: восьмизвенная ломаная на кубе для 5-7 классов
Задача
На поверхности куба проведена замкнутая восьмизвенная ломаная, вершины которой совпадают с вершинами куба.
Какое наименьшее количество звеньев этой ломаной может совпасть с рёбрами куба?
Решение
Звеньями ломаной являются либо рёбра куба, либо диагонали его граней. Для этого раскрасим вершины куба в два цвета в шахматном порядке (см. рис.). Заметим, что ребро куба соединяет вершины разных цветов, а диагональ – вершины одного цвета. Для того, чтобы ломаная прошла через все вершины, она должна в какой-то момент поменять цвет, а чтобы она была замкнутой, надо поменять цвет ещё раз. Значит, не менее двух раз звенья ломаной должны совпасть с рёбрами куба.
Этого достаточно, пример см. на рисунке.
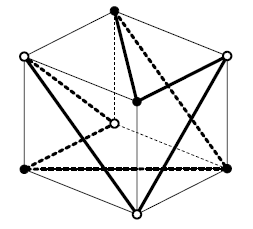
Ответ
Два звена.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь