Олимпиадная задача по планиметрии для 9-11 классов: площадь вписанного четырёхугольника

  Пусть диагонали АВСD пересекаются в точке Р. Докажем, что АС и BD перпендикулярны.   Первый способ. Используем очевидный факт: если АР – высота треугольника АВС, О – центр его описанной окружности, то  ∠ОАВ = ∠РАС  (рис. слева).

  Применив этот факт к треугольнику АВD (рис. справа), получим, что из условия  ∠ВАО = ∠DAC  и единственности перпендикуляра, опущенного из точки А на прямую BD, следует, что АР ⊥ BD.

  Второй способ. Проведём диаметр АА', тогда из равенства  ∠ВАО = ∠DAC  следует, что  ∠ВАР = ∠DAА'  (см. рис. б). Кроме того,  ∠АВР = ∠AА'D  (вписанные углы, опирающиеся на одну дугу). Так как вписанный угол ADA' опирается на диаметр, то  ∠ADA' = 90°,  значит,

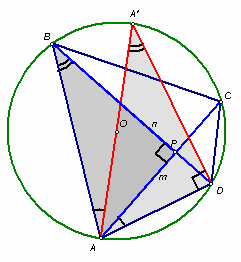
∠ВАР + ∠АВР = ∠DAА’ + ∠AА’D = 90°.  Таким образом, угол АРВ между диагоналями четырехугольника – прямой.

  Следовательно,  S_ABCD = ½ AC·BD = ^mn/₂.

^mn/₂.