Решение 1:   Лемма. Пусть точки X, Y принадлежат треугольнику ABC, но не совпадают с его вершинами, и отрезок XY не параллелен ни одной из сторон треугольника. Тогда от одной из вершин треугольника ABC можно отложить отрезок, равный и параллельный XY, так, что второй его конец окажется внутри треугольника.

  Доказательство. Проведём через вершины треугольника ABC прямые, параллельные XY. Одна из этих прямых лежит между двумя другими. Если, например, эта прямая проходит через вершину A, то она пересечёт сторону BC в некоторой точке D и разобьёт ABC на треугольники ABD и ACD. Отрезок XY лежит в одном из них и параллелен стороне AD, поэтому он короче AD. Значит, если отложить от точки A внутрь треугольника отрезок AZ, параллельный и равный XY, его конец Z окажется внутри треугольника ABC.

  Вернёмся к задаче. Пусть X и Y – два узла внутри треугольника ABC. Если прямая XY параллельна одной из сторон треугольника, все в порядке. В противном случае, точка Z, построенная согласно лемме, также является узлом. По условию она совпадает с одной из точек X или Y. Но тогда точки X и Y лежат на прямой, проходящей через соответствующую вершину треугольника.

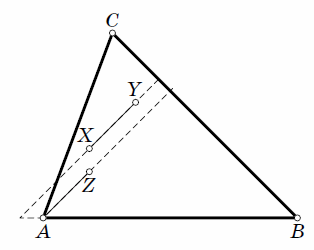
Решение 2:  Если прямаяXYне проходит через вершины треугольникаABC, то она не пересекает одну из его сторон, например,AB. Тогда внутри треугольниковAXBиAYBнет узлов, и поформуле Пика(см. задачу158208) площади треугольниковAXBиAYBравны. Значит, точкиXиYнаходятся на равных расстояниях от прямойAB, то есть прямаяXYпараллельна прямойAB(см. рис.).

Ответ задачи отсутствует