Решение 1:   Обозначим через A₁, B₁, C₁ соответственно середины сторон BC, CA и AB треугольника ABC. Возьмём два произвольных узла X и Y внутри треугольника. Пусть один из них лежит вне треугольника A₁B₁C₁, например, X лежит внутри треугольника AB₁C₁. Построим отрезок AW, серединой которого является точка X. Тогда W – также узел, он находится внутри ABC, и прямая XW проходит через A.

  Пусть теперь оба узла X и Y принадлежат треугольнику A₁B₁C₁. Если прямая XY параллельна одной из сторон треугольника, все в порядке. В противном случае применим лемму из решения задачи 132889 к треугольнику A₁B₁C₁. Пусть, например, конец Z₁ отрезка A₁Z₁, равного и параллельного XY, лежит внутри треугольника A₁B₁C₁. Тогда отрезок AZ, симметричный A₁Z₁ относительно середины B₁C₁, также равен и параллелен XY. Поэтому Z – узел, лежащий внутри AB₁C₁. Как показано выше, на прямой AZ есть ещё один узел.

Решение 2:   Рассмотрим данный треугольник ABC и узлы X и Z внутри него. Через X проведём три прямые, параллельные сторонам треугольника. Таким образом, треугольник ABC разбивается на три треугольника и три параллелограмма (см. рис.).

  1) Если Z лежит на одной из трёх прямых, то прямая XZ параллельна одной из сторон по построению.   2) Пусть Z лежит в одном из параллелограммов. Проведём через Z три прямые, параллельные сторонам треугольника. Тогда X относительно Z лежит в одном из трёх полученных треугольников. Заменой обозначений X и Z приходим к следующему случаю.   3) Допустим, Z лежит внутри одного из треугольников, скажем, TRX. Обозначим точку пересечения CX и AB буквой S и разберём два случая.

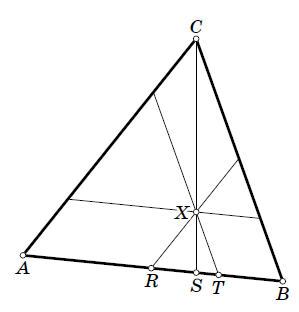
  3а)  CX ≥ XS.  Тогда обе точк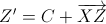и     и 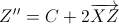    лежат внутри ABC. Эти точки являются узлами, так что пара  (Z', Z'')  – искомая.

  3б)  CX < XS.  Тогда узел     лежит внутри треугольника ABC, и подходит пара узлов  (X, Y).

Ответ задачи отсутствует