Задача
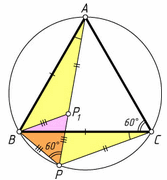
На дуге BC окружности, описанной около равностороннего треугольника ABC, взята произвольная точка P. Докажите, что AP = BP + CP.
Решение
Первый способ. Отложим на луче AP отрезок AP1, равный отрезку CP. Тогда треугольники AP1B и CPB равны по двум сторонам и углу между ними. В треугольнике BPP1 BP1 = BP, ∠BPP1 = ∠BPA = ∠BCA = 60°. Поэтому PP1 = BP. Следовательно, AP = AP1 + P1P = BP + CP.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет