Задача
Докажите, что если две биссектрисы треугольника равны, то он равнобедренный.
Решение
Первый способ.
Пусть $\alpha$, $\beta$, $\gamma$ — углы при вершинах соответственно A,
B и C треугольника ABC; BM и CN — биссектрисы треугольника. Предположим,
что
$\beta$ < $\gamma$.
Отложим от луча CN в полуплоскости, содержащей точку M, угол NCM1, равный ${\frac{\beta}{2}}$, где M1 — точка на биссектрисе BM. Поскольку ${\frac{\beta}{2}}$ < ${\frac{\gamma}{2}}$, то точка M1 лежит между точками B и M.
Отрезок NM1 виден из точек B и C под одним углом, равным
${\frac{\beta}{2}}$. Следовательно, точки B, N, M1 и C лежат на одной окружности, а BM1 и CN — хорды этой окружности. Поскольку
$\displaystyle \angle$BCM1 = $\displaystyle {\frac{\gamma}{2}}$ + $\displaystyle {\frac{\beta}{2}}$ < $\displaystyle {\frac{\alpha}{2}}$ + $\displaystyle {\frac{\beta}{2}}$ + $\displaystyle {\frac{\gamma}{2}}$ = 90o,
$\displaystyle \angle$BCM1 = $\displaystyle {\frac{\beta}{2}}$ + $\displaystyle {\frac{\gamma}{2}}$ > $\displaystyle \beta$ = $\displaystyle \angle$NBC,
то хордаBM1видна из точкиCпод острым
углом, равным${\frac{\gamma}{2}}$+${\frac{\beta}{2}}$, а хордаCNвидна из точкиBпод острым углом, равным$\beta$, причём${\frac{\beta}{2}}$+${\frac{\gamma}{2}}$>$\beta$. Следовательно,
BM > BM1 > CN.
Таким образом, если углы треугольника не равны, то большему
углу соответствует меньшая биссектриса. Следовательно, если
биссектрисы равны, то равны и соответствующие им углы
треугольника.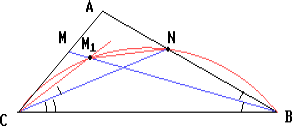
Второй способ.
Пусть a, b и c — стороны треугольника, $\beta$ и $\gamma$ — углы,
противолежащие сторонам b и c соответственно, lb и lc —
биссектрисы треугольника, проведённые из вершин этих углов.
По известной формуле для площади треугольника имеем:
$\displaystyle {\textstyle\frac{1}{2}}$ab sin$\displaystyle \gamma$ = $\displaystyle {\textstyle\frac{1}{2}}$blcsin$\displaystyle {\frac{\gamma}{2}}$ + $\displaystyle {\textstyle\frac{1}{2}}$alcsin$\displaystyle {\frac{\gamma}{2}}$,
откуда находим, что
lc = $\displaystyle {\frac{2ab \cos \frac{\gamma}{2}}{a + b}}$.
Ааналогично
lb = $\displaystyle {\frac{2ac \cos \frac{\beta}{2}}{b+c}}$.
Докажем, что еслиc>b, тоlc<lb.
В самом деле,
c > b $\displaystyle \Rightarrow$ $\displaystyle \gamma$ > $\displaystyle \beta$ $\displaystyle \Rightarrow$ $\displaystyle {\frac{\gamma}{2}}$ > $\displaystyle {\frac{\beta}{2}}$ $\displaystyle \Rightarrow$ cos$\displaystyle {\frac{\gamma}{2}}$ < cos$\displaystyle {\frac{\beta}{2}}$;
c > b $\displaystyle \Rightarrow$ a + c > a + b $\displaystyle \Rightarrow$ $\displaystyle {\frac{1}{a+c}}$ < $\displaystyle {\frac{1}{a+b}}$ $\displaystyle \Rightarrow$
$\displaystyle \Rightarrow$ $\displaystyle {\frac{a}{a+c}}$ < $\displaystyle {\frac{a}{a+b}}$ $\displaystyle \Rightarrow$ $\displaystyle {\frac{ab}{a+c}}$ < $\displaystyle {\frac{ac}{a+b}}$ $\displaystyle \Rightarrow$
$\displaystyle \Rightarrow$ lc = $\displaystyle {\frac{2ab \cos \frac{\gamma}{2}}{a + b}}$ < $\displaystyle {\frac{2ac \cos \frac{\beta}{2}}{a + c}}$ = lb.
Таким образом, если стороны треугольника не равны, то к
большей стороне проведена меньшая биссектриса. Следовательно,
если биссектрисы равны, то равны и соответствующие им стороны
треугольника.
Третий способ.
Выразим обе биссектрисы через стороны треугольника и
приравняем полученные выражения.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет