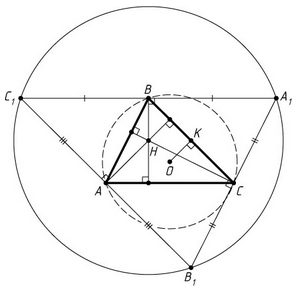
Для прямоугольного треугольника утверждение очевидно. Рассмотрим случай не прямоугольного треугольника. Пусть H – точка пересечения высот треугольника ABC, O – центр его описанной окружности, K – середина BC.   Первый способ. Проведём через вершины данного треугольника ABC прямые, параллельные противоположным сторонам. Получим новый треугольник, подобный данному с коэффициентом 2 (стороны треугольника ABC являются средними линиями нового треугольника). При этом высоты треугольника ABC лежат на серединных перпендикулярах нового треугольника (рис. слева).

  Отрезок AH в новом треугольнике соответствует отрезку OK в исходном треугольнике. Поэтому  AH = 2OK.

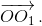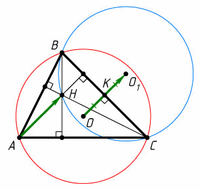
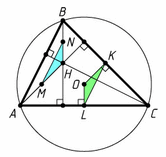
 Второй способ. Поскольку  ∠BHC= 180° – ∠A,  радиусы описанных окружностей треугольниковABCиHBCравны. Следовательно, эти окружности симметричны относительно прямойBC(рис. справа) и  OK=O₁K. С другой стороны, эти окружности переходят друг в друга при параллельном переносе на вектор    Следовательно, 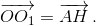   Поэтому  HA = OO₁= 2OK.   Третий способ. Пусть M, N, L – середины отрезков AH, BH и BC соответственно (рис. слева). Тогда  MN = KL  и  MN || KL  (средние линии треугольников ABH и ABC),  MH || OK,  NH || OL.

  Поэтому треугольники MNH и KLO равны по стороне и двум углам. Следовательно,  OK = MH = ^AH/₂.

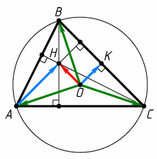
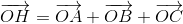  Четвёртый способ. Из равенства     (см. задачу 155367) следует, что  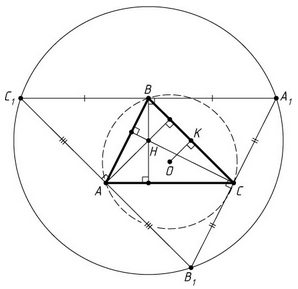   Пятый способ. Пусть A₁ – точка, диаметрально противоположная вершине A. Тогда  ∠ABA₁ = ∠ACA₁ = 90°,  а так как  BH ⊥ AC  и  CH ⊥ AB,  то  BH || CA  и

CH || BA₁.  Значит, BHCA₁ – параллелограмм. Его диагонали делятся точкой пересечения K пополам. При этом  OK ⊥ BC.  Отрезок OK – средняя линия треугольника AHA₁, следовательно,  OK = ^AH/₂.   Шестой способ. Пусть L и F – середины отрезков AC и CH соответственно. Тогда  OK ⊥ BC  и  AH ⊥ BC,  поэтому  OK || AH.  С другой стороны, LF – средняя линия треугольника AHC, поэтому  LF || AH  и  LF = ^AH/₂.  Следовательно,  LF || OK.  Отрезок KF – средняя линия треугольника BHC, поэтому  KF || BH,  а так как  BH ⊥ AC,  то  KF ⊥ AC.  С другой стороны,  OL ⊥ AC,  значит,  OL || KF.  Противоположные стороны четырёхугольника OKFL попарно параллельны, значит, это параллелограмм. Следовательно,  OK = LF = ^AH/₂.

Ответ задачи отсутствует