Задачи и олимпиады по математике

Задача

Докажите, что в любом треугольнике точка H пересечения высот (ортоцентр), центр O описанной окружности и точка M пересечения медиан (центр тяжести) лежат на одной прямой, причём точка M расположена между точками O и H, и MH = 2MO.

Решение

Первый способ.

Пусть A₁ — середина стороны BC треугольника ABC, G — точка пересечения прямых AA₁ и OH. Воспользуемся известным фактом: AH = 2OA₁.

Из подобия треугольников A₁GO и AGH следует, что

$\displaystyle {\frac{AG}{GA_{1}}}$ = $\displaystyle {\frac{HG}{GO}}$ = $\displaystyle {\frac{AH}{OA_{1}}}$ = 2.

Следовательно,G— точка пересечения медиан треугольникаABC, т.е.Gсовпадает сMиMH= 2MO.

Второй способ.

Пусть AA₁, BB₁ и CC₁ — медианы, а AA₂, BB₂ и CC₂ — высоты треугольника ABC. Рассмотрим гомотетию с центром в точке M и коэффициентом - ${\frac{1}{2}}$.

При этой гомотетии треугольник ABC переходит в треугольник

A₁B₁C₁, а прямые AA₂, BB₂ и CC₂ — в серединные перпендикуляры к сторонам треугольника ABC (высоты треугольника A₁B₁C₁). Поэтому точка H пересечения высот треугольника ABC переходит в точку пересечения серединных перпендикуляров этого треугольника, т.е. в центр O его описанной окружности. Следовательно, точки H и O лежат на прямой, проходящей через центр гомотетии (точку M), и MH = 2MO.

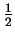
Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления