Пусть ABC – произвольный треугольник, H – точка пересечения его высот, l – прямая, проходящая через точку H, l_c и H_c – образы прямой l и точки H при симметрии относительно прямой AB, l_a и H_a – относительно BC, l_b и H_b – относительно AC.

  Заметим, что точки H_a, H_b, H_c лежат на описанной окружности треугольника ABC (см. задачу 155463).   Прямая l_b получена из прямой l_c композицией симметрий относительно прямых AB и AC, следовательно, угол между l_c и l_b равен 2∠A. Поскольку 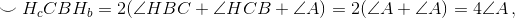    то прямые l_c и l_b пересекаются на описанной окружности треугольника ABC. Аналогично для прямых l_c, l_a и l_a, l_b.

  Прямые l_c, l_a и l_b пересекают окружность в точках H_c, H_a и H_b соответственно. Если треугольник не прямоугольный, то точки H_c, H_a и H_b различны. Следовательно, вторые точки пересечения этих прямых с окружностью совпадают. Поэтому все три прямые пересекаются на описанной окружности треугольника ABC.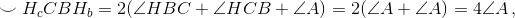

Ответ задачи отсутствует