Математическая задача: поворот кругового сегмента и перпендикуляры
Задача
Круг поделили хордой AB на два круговых сегмента и один из них повернули на некоторый угол вокруг точки A. При этом повороте точка B перешла в точку D (см. рис.).
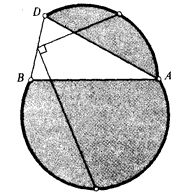
Решение
Пусть C и E – середины соответственно оставшейся на месте дуги AB и дуги AD, M – середина отрезка BD. Первый способ. Пусть K и H – середины отрезков AD и AB (см. рис.), F – диаметрально противоположна точке C (середина "старой" дуги AB). HM и KM – средние линии равнобедренного треугольника ABD, поэтому AKMH – ромб. Следовательно, EH ⊥ AD || KM, CK ⊥ AB || HM и ∠EHM = ∠MKC как углы с взаимно перпендикулярными сторонами. Кроме того, CH : HM = CH : AH = AH : HF = MK : KE, значит, треугольники CHM и MKE подобны. А так как у них две пары сторон взаимно перпендикулярны, то и третья тоже: EM ⊥ MC.
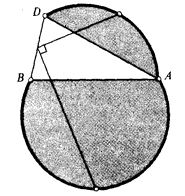
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь