Задача
На сторонах треугольникаABCвзяты точки A1,B1и C1, делящие его стороны в отношениях BA1:A1C=p,CB1:B1A=qи AC1:C1B=r. Точки пересечения отрезков AA1,BB1и CC1расположены так, как показано на рис. Найдите отношение площадей треугольников PQRи ABC.
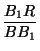
Решение
Воспользовавшись результатом задачи 1.3, легко проверить, что
$\displaystyle {\frac{BQ}{BB_1}}$ = $\displaystyle {\frac{p+pq}{1+p+pq}}$, $\displaystyle {\frac{B_1R}{BB_1}}$ = $\displaystyle {\frac{qr}{1+q+qr}}$, $\displaystyle {\frac{CR}{CC_1}}$ = $\displaystyle {\frac{q+qr}{1+q+qr}}$, $\displaystyle {\frac{CP}{CC_1}}$ = $\displaystyle {\frac{pr}{1+r+pr}}$.
Ясно также, что
$\displaystyle {\frac{S_{PQR}}{S_{RB_1C}}}$ = $\displaystyle {\frac{QR}{RB_1}}$ . $\displaystyle {\frac{PR}{RC}}$ и $\displaystyle {\frac{S_{RB_1C}}{S_{ABC}}}$ = $\displaystyle {\frac{B_1C}{AC}}$ . $\displaystyle {\frac{B_1R}{BB_1}}$.
Поэтому
$\displaystyle {\frac{S_{PQR}}{S_{ABC}}}$ = $\displaystyle {\frac{QR}{BB_1}}$ . $\displaystyle {\frac{PR}{RC}}$ . $\displaystyle {\frac{B_1C}{AC}}$ = $\displaystyle {\frac{QR}{BB_1}}$ . $\displaystyle {\frac{PR}{CC_1}}$ . $\displaystyle {\frac{CC_1}{CR}}$ . $\displaystyle {\frac{B_1C}{AC}}$.
Учитывая, что
$\displaystyle {\frac{QR}{BB_1}}$ = 1 - $\displaystyle {\frac{p+pq}{1+p+pq}}$ - $\displaystyle {\frac{qr}{1+q+rq}}$ = $\displaystyle {\frac{1}{1+p+pq}}$ - $\displaystyle {\frac{rq}{1+q+rq}}$ = $\displaystyle {\frac{(1+q)(1-pqr)}{(1+p+pq)(1+q+qr)}}$
и
$\displaystyle {\frac{PR}{CC_1}}$ = $\displaystyle {\frac{(1+r)(1-pqr)}{(1+q+qr)(1+r+pr)}}$,
получаем
$\displaystyle {\frac{S_{PQR}}{S_{ABC}}}$ = $\displaystyle {\frac{(1-pqr)^2}{(1+p+pq)(1+q+qr)(1+r+pr)}}$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет