Правильный восьмиугольник и его диагонали — задание олимпиады
Задача
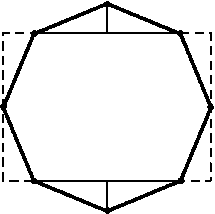
Докажите, что площадь правильного восьмиугольника равна произведению длин наибольшей и наименьшей его диагоналей.
Решение
Отрежем от правильного восьмиугольника треугольники и переставим их так, как показано на рис. В результате получим прямоугольник, стороны которого равны наибольшей и наименьшей диагоналям восьмиугольника. Тогда B1C1= 2 sin(A/2), а значит, 2 sin(A/2)Ra$\geq$dc+db. Умножая это неравенство на аналогичные неравенства для Rbи Rcи учитывая, что sin(A/2)sin(B/2)sin(C/2) =r/4R(задача 12.36, а)), получаем требуемое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет