Задача
Пусть α, β и γ - углы треугольника ABC. Докажите, что а) sin($\alpha$/2)sin($\beta$/2)sin($\gamma$/2) =r/4R; б) tg($\alpha$/2)tg($\beta$/2)tg($\gamma$/2) =r/p; в) cos($\alpha$/2)cos($\beta$/2)cos($\gamma$/2) =p/4R.
Решение
а) Пусть O — центр вписанной окружности, K — точка касания вписанной окружности со стороной AB. Тогда
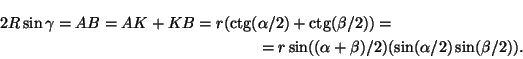
Учитывая, что sin$\gamma$= 2 sin($\gamma$/2)cos($\gamma$/2) и sin(($\alpha$+$\beta$)/2) = cos($\gamma$/2), получаем требуемое. б) Согласно задаче 3.2 p-a=AK=rctg($\alpha$/2). Аналогично p-b=rctg($\beta$/2) и p-c=rctg($\gamma$/2). Перемножая эти равенства и учитывая, что p(p-a)(p-b)×(p-c) =S2= (pr)2, получаем требуемое. в) Очевидным образом следует из задач а) и б).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет