Задача
На сторонах AB и BC остроугольного треугольника ABC внешним образом построены квадраты ABC1D1 и A2BCD2.
Докажите, что точка пересечения прямых AD2 и CD1 лежит на высоте BH.
Решение
Обозначим через a, b, c длины сторон, а через α, β, γ – соответствующие углы треугольника ABC. Пусть X – точка пересечения прямых AD2 и CD1; M, E1 и E2 – проекции точек X, D1 и D2 на прямую AC. Тогда
CE2 = a sin γ и AE1 = c sin α. Так как a sin γ = c sin α, то CE2 = AE1 = q. Поэтому 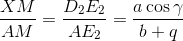 и
и 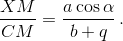 .
.
Следовательно, AM : CM = c cos α : a cos γ. Высота BH делит сторону AC в таком же отношении.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет