Задача
Окружность S касается окружностей S1 и S2 в точках A1 и A2.
Докажите, что прямая A1A2 проходит через точку пересечения общих внешних или общих внутренних касательных к окружностям S1 и S2.
Решение
Пусть O, O1 и O2 – центры окружностей S, S1 и S2; X – точка пересечения прямых O1O2 и A1A2. Применяя теорему Менелая к треугольнику OO1O2 и точкам A1, A2 и X, получаем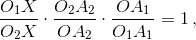 
а значит, O1X : O2X = R1 : R2, где R1 и R2 –
радиусы окружностей S1 и S2. Следовательно, X – точка пересечения общих внешних или общих внутренних касательных к окружностям S1 и S2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет