Задача
На сторонеBCтреугольникаABCвзяты точкиK1иK2. Докажите, что общие внешние касательные к вписанным окружностям треугольниковABK1иACK2общие внешние касательные к вписанным окружностям треугольниковABK2иACK1пересекаются в одной точке.
Решение
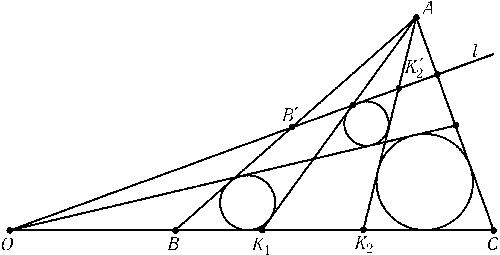
ПустьO — точка пересечения общих внешних касательных к вписанным окружностям треугольниковABK1иACK2(рис.). Проведем из точкиOкасательнуюlк вписанной окружности треугольника, образованного прямымиAK1,AK2и касательной к вписанным окружностям треугольниковABK1иACK2, отличной от прямойBC. Пусть прямаяlпересекает прямыеABиAK2в точкахB'иK2'. Согласно задаче6.12четырехугольникBK2K2'B'описанный. Это означает, что прямаяlкасается вписанной окружности треугольникаABK2. Аналогично доказывается, что прямаяlкасается вписанной окружности треугольникаACK1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь