Точки A₁,A₂и A₃лежат на прямыхP₂P₃,P₃P₁и P₁P₂(рис.), поэтому описанные окружности треугольниковA₁A₂P₃,A₁A₃P₂и A₂A₃P₁имеют общую точку V(см. задачу 2.80, а)), причем точки O₃,O₂и O₁лежат на этих окружностях (см. задачу 19.41). Аналогично описанные окружности треугольниковB₁B₂P₃,B₁B₃P₂и B₂B₃P₁имеют общую точку V'. Пусть U — точка пересечения прямыхP₂O₂и P₃O₃. Докажем, что точка Vлежит на описанной окружности треугольникаO₂O₃U. В самом деле,$\angle$(O₂V,VO₃) =$\angle$(VO₂,O₂P₂) +$\angle$(O₂P₂,P₃O₃) +$\angle$(P₃O₃,O₃V) =$\angle$(VA₁,A₁P₂) +$\angle$(O₂U,UO₃) +$\angle$(P₃A₁,A₁V) =$\angle$(O₂U,UO₃). Аналогичные рассуждения показывают, что точка V'лежит на описанной окружности треугольникаO₂O₃U. В частности, точки O₂,O₃,Vи V'лежат на одной окружности. Аналогично точки O₁,O₂,Vи V'лежат на одной окружности, а значит, точки Vи V'лежат на описанной окружности треугольникаO₁O₂O₃; точка Uтоже лежит на этой окружности. Аналогично доказывается, что прямыеP₁O₁и P₂O₂пересекаются в точке, лежащей на окружности подобия. ПрямаяP₂O₂пересекает окружность подобия в точках Uи O₂, поэтому прямаяP₁O₁проходит через точку U.

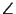
Ответ задачи отсутствует