Олимпиадная задача о формулах площадей пересечений фигур
Задача
На плоскости дано n фигур. Пусть Si1...ik – площадь пересечения фигур с номерами i1, ..., ik, a S – площадь части плоскости, покрытой данными фигурами; Mk – сумма всех чисел Si1...ik. Докажите, что:
а) S = M1 – M2 + M3 – ... + (–1)n + 1Mn;
б) S ≥ M1 - M2 + M3 – ... + (–1)m + 1Mm при m чётном и
S ≤ M1 – M2 + M3 – ... + (–1)m + 1Mm при m нечётном.
Решение
Решение 1: а) Обозначим через Wm площадь части плоскости, покрытой ровно m фигурами. Эта часть состоит из кусков, каждый из которых покрыт какими-то определенными m фигурами. Площадь каждого такого куска при вычислении Mk учитывается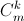 
раз. Поэтому
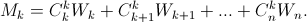
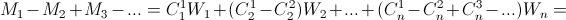
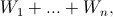
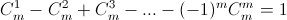(см. задачу160412).
Остается заметить, что S=W1+ ... +Wn. б) Согласно а)
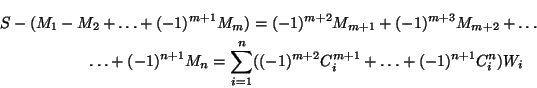
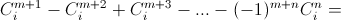
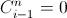при i≤n.
Решение 2: а) Индукция по n. База (n = 1) очевидна.
Шаг индукции. Пусть для n фигур формула доказана. Рассмотрим фигуры A1, ..., An, An+1 и обозначим A = A1 ∪ ... ∪ An, Bi = Ai ∩ An+1,
S = S(A) – площадь фигуры A, S′ = S(A ∪ An+1). Ясно, что S′ = S + S(An+1) – S(A ∩ An+1).
По предположению индукции
S = M1 – M2 + M3 – ... – (–1)nMn ;
S(A ∩ An+1) = S(B1 ∪ ... ∪ Bn) = N1 – N2 + N3 – ... – (–1)nNn ,
где Nn – сумма площадей всех фигур вида Bi1 ∩ ... ∩ Bik = Ai1 ∩ ... ∩ Aik ∩ An+1 . Поэтому
,
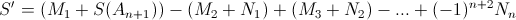
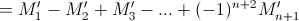где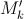 
– сумма площадей всевозможных пересечений k из наших n + 1 фигур. б) Индукция проводится аналогично а). Пусть, например, m четно. Тогда (в тех же обозначениях)
S ≥ M1 – M2 + M3 – ... – Mm ,
S(A ∩ An+1) ≤ N1 – N2 + N3 – ... + Nm–1 .
Поэтому
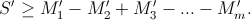
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь