Олимпиадная задача по комбинаторной геометрии — неравенство для узлов
Задача
Внутри выпуклой фигуры с площадью Sи полупериметром pлежит nузлов решетки. Докажите, чтоn>S-p.
Решение
Рассмотрим целочисленную решетку, заданную уравнениямиx=k+ 1/2 и y=l+ 1/2, где kи l — целые числа. Докажем, что каждый квадрат этой решетки дает неотрицательный вклад в величинуn-S+p. Рассмотрим два случая.
- Фигура содержит центр квадрата. Тогдаn'= 1 и S'$\le$1, поэтомуn'-S'+p'$\ge$0.
- Фигура пересекает квадрат, но не содержит его центр. Докажем,
что в этом случаеS'$\le$p'. Если фигура целиком лежит в этом квадрате, то
согласно изопериметрическому неравенствуS'/p'$\le$
 $\le$$\sqrt{1/\pi}$< 1. Если рассматриваемая часть фигуры
ограничена стороной квадрата и некоторой кривой, то согласно
задаче 22.BIs15aS'/p'$\le$
$\le$$\sqrt{1/\pi}$< 1. Если рассматриваемая часть фигуры
ограничена стороной квадрата и некоторой кривой, то согласно
задаче 22.BIs15aS'/p'$\le$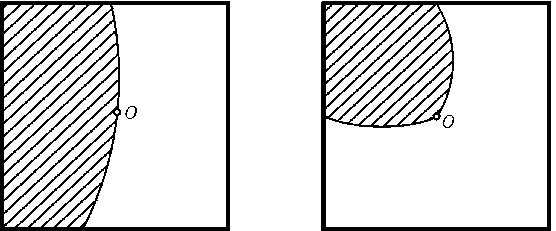 $\le$$\sqrt{2/\pi}$< 1.
Поэтому остаётся рассмотреть случаи, когда
рассматриваемая часть фигуры ограничена сторонами квадрата и кривой,
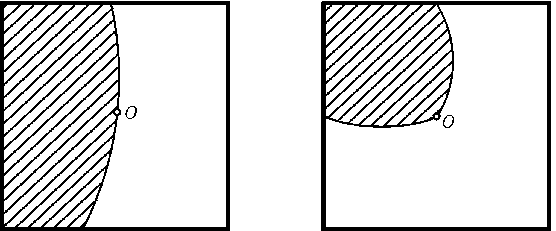
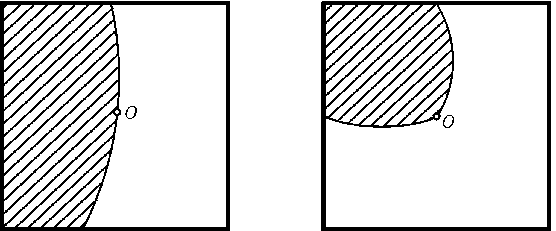
соединяющей либо противоположные, либо смежные стороны квадрата. При этом можно
считать, что центрOквадрата лежит на границе фигуры (рис.).
Действительно, для кривой, соединяющей противоположные стороны, можно применить
параллельный перенос, а для кривой, соединяющей смежные стороны, — гомотетию
с центром в их общей вершине. В обоих случаях отношениеS'/p'увеличится.
Так как расстояния от центра квадрата до его сторон равны 1/2, тоp'$\ge$1/2. Проведя через точку Oопорную прямую к данной фигуре, получим,
чтоS'$\le$1/2.
Ясно также, что все вклады квадратов не могут быть одновременно нулевыми.
$\le$$\sqrt{2/\pi}$< 1.
Поэтому остаётся рассмотреть случаи, когда
рассматриваемая часть фигуры ограничена сторонами квадрата и кривой,
соединяющей либо противоположные, либо смежные стороны квадрата. При этом можно
считать, что центрOквадрата лежит на границе фигуры (рис.).
Действительно, для кривой, соединяющей противоположные стороны, можно применить
параллельный перенос, а для кривой, соединяющей смежные стороны, — гомотетию
с центром в их общей вершине. В обоих случаях отношениеS'/p'увеличится.
Так как расстояния от центра квадрата до его сторон равны 1/2, тоp'$\ge$1/2. Проведя через точку Oопорную прямую к данной фигуре, получим,
чтоS'$\le$1/2.
Ясно также, что все вклады квадратов не могут быть одновременно нулевыми.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет