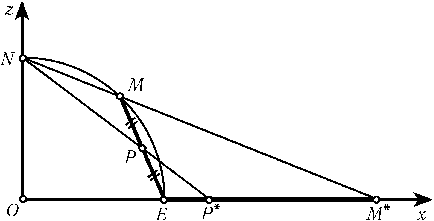
а) Рассмотрим на координатной плоскостиOxzточкиO(0, 0),N(0, 1),E(1, 0). Для произвольной точки M, лежащей на
дугеNEединичной окружности (см. рис.), обозначим через Pсередину отрезкаEM, а через Mи P — точки пересечения
прямыхNMи NPсоответственно с прямойOE.
Докажем, что для любого числаk> 2 можно выбрать точку Mтаким образом, чтоME:PE=k. ПустьA(a,b) —
произвольная точка плоскости,A*(t, 0) — точка
пересечения прямыхNAи OE,B(0,b) — проекция точки Aна прямуюON. Тогда
t = $\displaystyle {\frac{A^*O}{ON}}$ = $\displaystyle {\frac{AB}{BN}}$ = $\displaystyle {\frac{a}{1-b}}$.
Поэтому, если (
x,
z) — координаты точки
M, то точки
P,
M*,
P*имеют соответственно координаты
P$\displaystyle \left(\vphantom{\frac{x+1}{2},\frac{z}{2}}\right.$$\displaystyle {\frac{x+1}{2}}$,$\displaystyle {\frac{z}{2}}$$\displaystyle \left.\vphantom{\frac{x+1}{2},\frac{z}{2}}\right)$, M*$\displaystyle \left(\vphantom{\frac{x}{1-z},0 }\right.$$\displaystyle {\frac{x}{1-z}}$, 0$\displaystyle \left.\vphantom{\frac{x}{1-z},0 }\right)$, P*$\displaystyle \left(\vphantom{\frac{(x+1)/2}{1-(z/2)},0}\right.$$\displaystyle {\frac{(x+1)/2}{1-(z/2)}}$, 0$\displaystyle \left.\vphantom{\frac{(x+1)/2}{1-(z/2)},0}\right)$,
значит,
M*E : P*E = $\displaystyle \left(\vphantom{\frac{x}{1-z}-1}\right.$$\displaystyle {\frac{x}{1-z}}$ - 1$\displaystyle \left.\vphantom{\frac{x}{1-z}-1}\right)$ : $\displaystyle \left(\vphantom{
\frac{x+1}{2-z}-1}\right.$$\displaystyle {\frac{x+1}{2-z}}$ - 1$\displaystyle \left.\vphantom{
\frac{x+1}{2-z}-1}\right)$ = $\displaystyle {\frac{x+z-1}{1-z}}$ : $\displaystyle {\frac{x+z-1}{2-z}}$ = $\displaystyle {\frac{2-z}{1-z}}$.
Ясно, что уравнение(2 -
z)/(1 -
z) =
kимеет решение
z= (
k- 2)/(
k- 1),
причем если
k> 2, то 0 <
z< 1, и, следовательно, точка
M($\sqrt{1-z^2}$,
z) требуемая.
Докажем теперь основное утверждение задачи. Обозначим данные
окружность и точку внутри ее соответственно через
Sи
C. Если
точка
Cявляется центром окружности
S, то требуемым проективным
преобразованием является тождественное преобразование. Поэтому
будем считать, что
Cне центр. Обозначим через
ABдиаметр,
содержащий точку
C. Пусть для определенности
BC>
CA. Положим
k=
BA:
AC. Тогда
k> 2, и, следовательно, как было доказано, на
единичной окружности в плоскости
Oxzможно расположить точку
Mтак, что
M*E:
P*E=
k=
BA:
CA. Поэтому преобразованием
подобия окружность
Sможно перевести в окружность
S1, построенную
в плоскости
Oxyна отрезке
EM*как на диаметре, так, чтобы
точки
A,
B,
Cперешли соответственно в точки
E,
M*,
P*.
При стереографической проекции окружность
S1проецируется
в окружность
S2на единичной сфере, которая симметрична относительно
плоскости
Oxz, а значит, и относительно прямой
EM. Поэтому
EM — диаметр окружности
S2, а его середина — точка
P — ее центр. Пусть $\alpha$ — плоскость, содержащая окружность
S2.
Ясно, что при центральном проектировании плоскости
Oxyна
плоскость $\alpha$из северного полюса единичной сферы окружность
S1перейдет в
S2, а точка
P* — в ее центр
P.
б) Диаметр
AB, проходящий через
M, переходит в диаметр.
Поэтому касательные в точках
Aи
Bпереходят в касательные.
Но если параллельные прямые переходят в параллельные, то
исключительная прямая им параллельна (см. задачу
30.14, в)).