Олимпиадная задача по планиметрии о четырехугольниках KLMN и K'L'M'N'
Задача
Пусть стороны самопересекающихся четырехугольниковKLMNиK'L'M'N', вписанных в одну и ту же окружность, пересекают хордуABэтой окружности в точкахP,Q,R,SиP',Q',R',S'соответственно (сторонаKL — в точкеP,LM — в точкеQ, и т. д.). Докажите, что если три из точекP,Q,R,Sсовпадают с соответственными тремя из точекP',Q',R',S', то и оставшиеся две точки тоже совпадают. (Предполагается, что хордаABне проходит через вершины четырехугольников.)
Решение
Пусть для определенностиP=P',Q=Q'иR=R'. Согласно задаче 31.051
$\displaystyle \lambda$lKLlMN + $\displaystyle \mu$lKNlML = f = $\displaystyle \lambda{^\prime}$lK'L'lM'N' + $\displaystyle \mu{^\prime}$lK'N'lM'L'.
Рассмотрев ограничение этого равенства на прямуюAB, получим равенство вида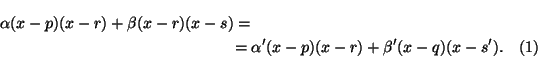
При этом требуется доказать, чтоs=s'. Равенство (1) можно преобразовать к виду
$\displaystyle \alpha{^\prime}{^\prime}$(x - p)(x - r) = (x - q)[$\displaystyle \beta$(x - s) - $\displaystyle \beta{^\prime}$(x - s')].
ТочкаQможет совпасть только с точкойS, поэтомуQ$\ne$PиQ$\ne$R, а
значит,(x-p)(x-r) не делится на (x-q). Поэтому$\beta$(x-s) -$\beta{^\prime}$(x-s') = 0. Следовательно,s=s'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет