Задача
Пусть τ(n) – количество положительных делителей натурального числа n =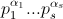 
, а σ(n) – их сумма. Докажите равенства:
а) τ(n) = (α1 + 1)...(αs + 1); б) σ(n) =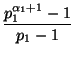 
·...·
.
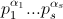Решение
б) Рассмотрим выражение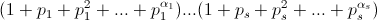 
.
Каждый одночлен, который получится при раскрытии скобок в этом выражении, – один из делителей числа n. При этом, очевидно, каждый делитель встречается в полученной сумме ровно один раз. Поэтому сумма делителей равна значению этого выражения, то есть 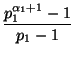·...·.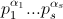 а) Количество делителей равно числу одночленов, которое мы получим, если заменим в каждой скобке все слагаемые на 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет