Математическая задача олимпиады о неравенстве для p и q
Задача
Докажите, что для любых целых чисел p и q (q ≠ 0), справедливо неравенство 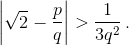
Решение
Предположим, что 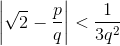 для некоторой дроби p/q. Согласно задаче 160619 число p/q является подходящей дробью Pn/Qn к
для некоторой дроби p/q. Согласно задаче 160619 число p/q является подходящей дробью Pn/Qn к ![]() .
.
Рассмотрим последовательность чисел qn – |Pn+kQn – PnQn+k|. Она удовлетворяет начальным условиям q0 = 0, q1 = 1 и рекуррентному соотношению qk = 2qk–1 + qk–2 (k ≥ 2). Поэтому числа qn совпадают
со знаменателями подходящих дробей к ![]() :
qk = Qk–1 (k ≥ 1), то есть
:
qk = Qk–1 (k ≥ 1), то есть 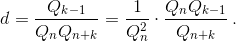
Чтобы получить противоречие с исходным предположением, достаточно
доказать неравенство 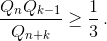
Свойства чисел Qn похожи на свойства чисел Фибоначчи. В частности, для них можно доказать равенство, аналогичное соотношению из задачи 160566:
Qn+k = Qk–1Qn+1 – Qk–2Qn. Поэтому 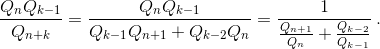
Остается заметить, что Qn+1/Qk ≤ 5/2 и Qk–2/Qk–1 ≤ 1/2 .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь