Задача
Когда 4p³ + 27q² < 0, уравнение x³ + px + q = 0 имеет три действительных корня (неприводимый случай кубического уравнения), но для того, чтобы их найти по формуле Кардано, необходимо использование комплексных чисел. Однако можно указать все три корня в явном виде через тригонометрические функции.
а) Докажите, что при p < 0 уравнение x³ + px + q = 0 заменой x = kt сводится к уравнению 4t³ – 3t – r = 0 (*) от переменной t.
б) Докажите, что при 4p³ + 27q² ≤ 0 решениями уравнения (*) будут числа t1 = cos
, t2 = cos
, t3 = cos
, где φ = arccos r.
Решение
а) После замены x = kt мы получим уравнение k³t³ + kpt + q = 0. Нам нужно, чтобы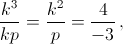 
поэтому можно взять 
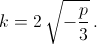Подставив и разделив на ¼ k³, получим 
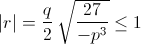при 4p³ + 27q² ≤ 0. б) 4 cos³α – 3 cos α – cos 3α = 0. Поэтому при подстановке в левую часть уравнения (*) любого из чисел t1, t2, t3, получим ноль. Поскольку |r| ≤ 1, то arccos r определен.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь