Задача
Диагонали вписанного четырёхугольника ABCD пересекаются в точке O. Описанные окружности треугольников AOB и COD пересекаются в точке M на стороне AD. Докажите, что точка O – центр вписанной окружности треугольника BMC.
Решение
Решение 1:Из равенства вписанных углов следует, что ∠OBC = ∠DBC = ∠DAC = ∠MAO = ∠MBO (см. рис.), то есть BO – биссектриса угла MBC. Аналогично CO – биссектриса угла BCM. Следовательно, O – центр вписанной окружности треугольника BMC.
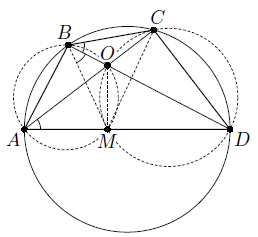
Решение 2:∠AMO = ∠DCO = ∠DCA = ∠DBA = ∠OBA = ∠DMO. Отсюда следует, что все эти углы – прямые. Значит, DB и AC – высоты треугольника, образованного прямыми AB, DC и AD, ортоцентр O которого является центром вписанной окружности ортотреугольника BMC (см. задачу 152866).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь