Пусть  n ≥ 2,  и  2 = p₁ < ... < p_k – первые k простых чисел. Предположим, что  p₁p₂...p_k = aⁿ + 1.     (*)

  Если  a = 1,  то  aⁿ + 1 = 2  и, следовательно,  k = 1.

  Предположим теперь, что  a > 1;  тогда  k > 1.  Число a нечётно, поэтому у него существует нечётный простой делитель q. Тогда  q > p_k,  иначе левая часть равенства (*) делилась бы на q, что не так. Поэтому и  a > p_k.

  Без ограничения общности можно считать, что n – простое число (если  n = st,  то можно заменить n на t, а a – на a^s). Заметим, что  n > 2,  поскольку

 a² + 1  не может делиться на  3 = p₂.

  Покажем, что  n > p_k.  Действительно, в противном случае  n = p_i,  где  i ≤ k.  Тогда  a^p_i + 1  кратно p_i; с другой стороны, по малой теореме Ферма  a^p_i – a  кратно p_i. Так как  a^p_i + 1 = (a + 1)(a^p_i–1 – a^p_i–2 + ... – a + 1),  причём  a + 1 = (a^p_i + 1) – (a^p_i – a)  кратно p_i и  a^p_i–1 – a^p_i–2 + ... – a + 1 ≡ 1 + 1 + ... + 1 = p_i ≡ 0 (mod p_i),  то   a^p_i + 1  делится на 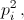    что противоречит условию.  Итак,  a > p_k  и  n > p_k,  откуда  aⁿ+ 1 >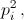>p₁p₂...p_k,  что противоречит равенству (*).

k = 1.