Задача
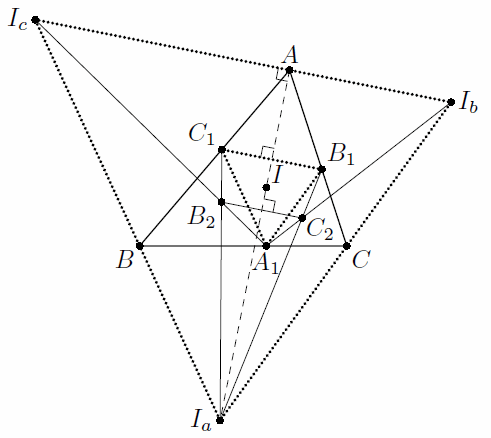
Окружность с центром I, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках A1, B1, C1 соответственно. Пусть Ia, Ib, Ic – центры вневписанных окружностей треугольника ABC, касающихся соответственно сторон BC, CA, AB. Отрезки IaB1 и IbA1 пересекаются в точке C2. Аналогично отрезки IbC1 и IcB1 пересекаются в точке A2, а отрезки IcA1 и IaC1 – в точке B2. Докажите, что I является центром описанной окружности треугольника A2B2C2.
Решение
Треугольники A1C1B2 и IcIaB2 подобны (A1C1 || IcIa как перпендикуляры к биссектрисе угла B). Аналогично подобны треугольники A1B1C2 и IbIaC2. Отсюда 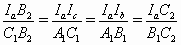 . Точки B1 и C1 симметричны относительно прямой AIa; а поскольку
. Точки B1 и C1 симметричны относительно прямой AIa; а поскольку 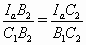 , точки B2 и C2 также симметричны относительно неё, и IB2 = IC2. Аналогично IA2 = IC2, что и требовалось доказать.
, точки B2 и C2 также симметричны относительно неё, и IB2 = IC2. Аналогично IA2 = IC2, что и требовалось доказать.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь