Задача
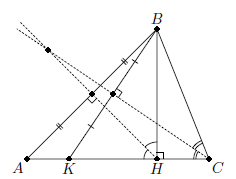
В треугольнике ABC ∠A = 45°, BH – высота, точка K лежит на стороне AC, причём BC = CK.
Докажите, что центр описанной окружности треугольника ABK совпадает с центром вневписанной окружности треугольника BCH.
Решение
Поскольку треугольник BCK – равнобедренный, то серединный перпендикуляр к стороне BK совпадает с биссектрисой угла ACB (см. рис.). Треугольник AHB – также равнобедренный, поэтому серединный перпендикуляр к стороне AB совпадает с биссектрисой угла AHB. Следовательно, центр описанной окружности треугольника ABK совпадает с точкой пересечения биссектрис внутреннего и внешнего углов треугольника BCH, то есть с центром его вневписанной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет