Решение 1:   Обозначим через C' точку касания вписанной окружности со стороной AB. Сделаем инверсию с центром в точке B'. Будем обозначать образы точек индексами "1", то есть образом точки A' будет A'₁ и т.п. Тогда образами прямых AB и BC будут окружности A₁B₁B' и C₁B₁B', а образом вписанной окружности – прямая A'₁C'₁, касающаяся обеих этих окружностей. Радикальная ось B'B₁ этих окружностей, содержащая точку G₁, делит отрезок A'₁C'₁ пополам.

  Отсюда вытекает следующее построение. Построим l₁ – образ прямой B'G (на которой лежит B₁) при гомотетии с центром A'₁ и коэффициентом 2; эта прямая содержит C'₁. Значит, её инверсный образ содержит точку C'. Проведя аналогичное построение, начиная с инверсии в точке A', получим вторую окружность, содержащую C', и, значит, сможем восстановить точку C' (вообще говоря, двумя способами). После этого восстанавливаются описанная окружность треугольника A'B'C' и стороны исходного треугольника, являющиеся касательными к ней.

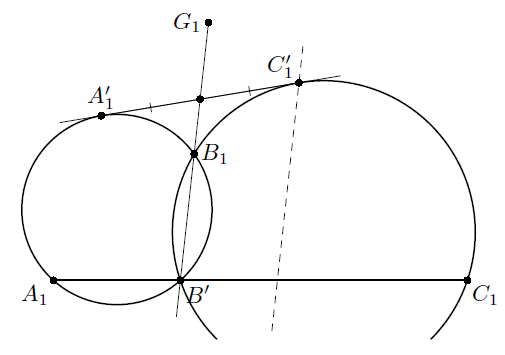
Решение 2:   Пусть C' – точка касания вписанной окружности со стороной AB, A₁, B₁, C₁ – проекции G на стороны треугольника A'B'C'. Прямые A'A, B'B, C'C являются симедианами треугольника A'B'C' (см. задачу 156983) и потому пересекаются в его точке Лемуана G. Согласно задаче 156991 G является точкой пересечения медиан треугольника A₁, B₁, C₁.

  Отсюда получаем следующее построение. Построим точку C₁ и ее образ C₂ при гомотетии с центром G и коэффициентом –½ (таким образом, C₂ – середина A₁B₁). Далее построим окружности ω_A, ω_B с диаметрами GA', GB'. Точка пересечения окружности ω_A с окружностью, симметричной ω_B относительно C₂, – это B₁ (вообще говоря, таких точек две). Точка A₁ симметрична ей относительно C₂. Теперь можно восстановить прямые A'C' и B'C' как перпендикуляры к GA₁ и GB₁ в точках A₁ и B₁; дальнейшее ясно.

Ответ задачи отсутствует