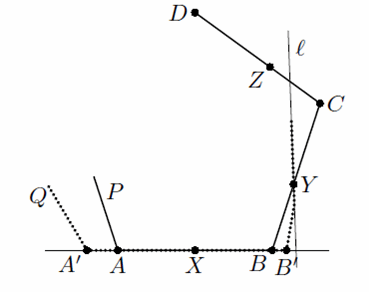
Пример. Докажем, что пяти точек достаточно. Пусть A, B, C, D – четыре последовательные вершины многоугольника (возможно,  A = D).  Отметим точки A, B, произвольную точку X на стороне AB, точку Y на стороне BC, достаточно близкую к B, и точку Z на стороне CD, достаточно близкую к C.

  Пусть P – исходный многоугольник, Q – некоторый правильный многоугольник, содержащий на периметре наши пять точек, α и β – углы этих многоугольников. Прямая AB должна содержать сторону многоугольника Q, так как на ней лежат три отмеченных точки. Пусть эта сторона – A'B'. Далее, пусть сторона Q, содержащая Y, лежит на прямой l; тогда точки B и Z должны лежать по одну сторону от неё (см. рис.).

  Поскольку Z близка к C, это означает, что угол между прямыми l и BC мал. С другой стороны,  α = ∠ABY ≥ ∠A'B'Y ≥ β,  то есть количество сторон у Q не больше, чем у P. Значит, угол между l и BC может быть достаточно мал лишь тогда, когда эти прямые совпадают. Итак, прямая BC также содержит сторону Q, а точка B тогда является его вершиной. Отсюда следует, что P и Q гомотетичны с центром в точке B, и контур Q может содержать Z только тогда, когда P совпадает с Q.   Оценка. Докажем, что при достаточно большом числе сторон n правильного многоугольника P четырёх точек не хватит для его задания. Предположим, что три из этих точек лежат на одной стороне AB многоугольника P. Правильный треугольник, построенный на AB, лежит целиком внутри P, то есть четвёртая из отмеченных точек лежит вне его. Поэтому, применив к нашему треугольнику гомотетию с центром в середине AB и подходящим коэффициентом, большим 1, можно добиться того, что и четвёртая отмеченная точка окажется на его контуре. Значит, в этом случае многоугольник однозначно не восстанавливается.

  Если же наше предположение неверно, то отмеченные точки образуют выпуклый четырёхугольник ABCD, "достаточно близкий" к вписанному. Именно, покажем, что  ∠A + ∠C ≥ 180° – ^360°/_n.  Пусть точки B и C лежат на сторонах KL и MN многоугольника P, причём точки A, K и N лежат по одну сторону от BD (см. рис.).

  Опишем вокруг P окружность ω с центром O. Тогда  ∠A + ∠C ≥ ∠LAM + ∠KCN = ½ (∠LOM + ∠KON) = 180° – ^360°/_n.  Аналогично,

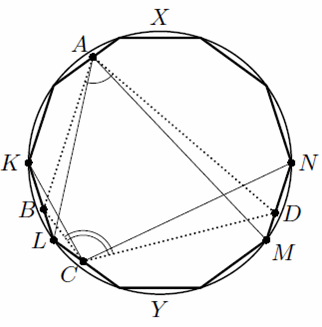
∠B + ∠D ≥ 180° – ^360°/_n,  то есть  ∠A + ∠C ≤ 180° + ^360°/_n.

  Мы покажем, что ABCD можно вписать либо в квадрат, либо в правильный треугольник. Пусть угол A – наибольший угол четырёхугольника ABCD, а  ∠B ≥ ∠D.  Возможны несколько случаев.

  1)  ∠B ≥ 90°.  Тогда ясно, что ABCD можно вписать в квадрат так, чтобы точки A, B попали на одну из сторон – одним из способов, изображённых на рисунке, в зависимости от того, что больше: проекция CD на AB или проекция ABCD на прямую, перпендикулярную AB).

  2)  ∠B < 90°, но при этом обе суммы  ∠A + ∠D  и  ∠B + ∠C  не превосходят 240°. Проведём через C и D прямые, составляющие с AB углы 60°. Тогда из наших неравенств следует, что все точки A, B, C, D лежат на сторонах этого треугольника.   3)  ∠B < 90°  (а значит, оба угла B и D близки к 90°), но  ∠A + ∠D > 240°  (поскольку угол A – наибольший, ∠B +  ∠C < 240°).  Покажем, что в этом случае можно вписать ABCD в квадрат так, как показано на рисунке.   Пусть X и Y – проекции точек C и D на AB; достаточно проверить, что  YB ≤ CX.  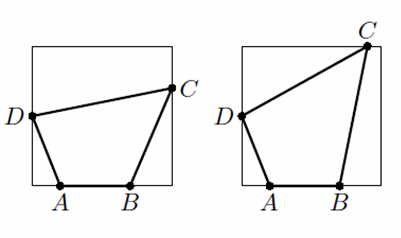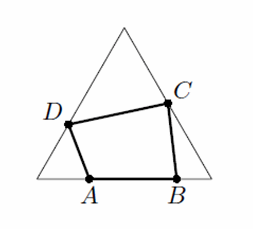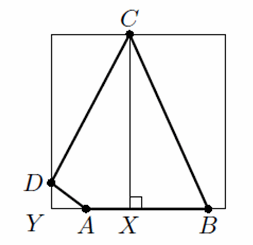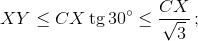Но  ∠DCX = 270° – (∠A + ∠D) ≤ 30°,  поэтому     с другой стороны,  ∠B ≥ ½ (∠B + ∠D) ≥ 90° – ^180°/_n,  то есть при большом n  tg∠B ≥ 10;  значит,

XB = CX ctg∠B ≤ ^CX/₁₀, и 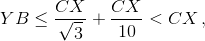    что и требовалось.

k = 5.