Пусть точка X пересечения AM и высоты CH треугольника ABC лежит на отрезке AM (см. рис.; в конце решения мы покажем, что другой случай невозможен).

  Из условия следует, что  ∠BAX = 30°.  Поэтому  ∠CXM = ∠AXH = 90° – ∠XAH = 60°.  Поскольку CH также является медианой треугольника ABC, то треугольник AXB – равнобедренный, то есть  ∠BXH = 60°.  Следовательно, и  ∠BXM = 60°.

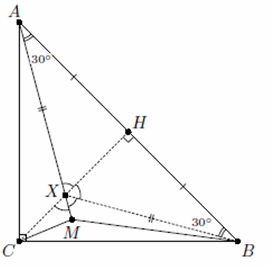
  Рассмотрим отдельно треугольник CXB. В нём  ∠XCB = 45°,  ∠XBC = 15°,  ∠CXB = 120°  и XM – биссектриса угла CXB (см. рис.).

  Обозначим  ∠MBC= α,  тогда  ∠MCB= 15° + α.  Выберем на отрезкеXBтакую точкуY, что  ∠YCB= 15°,  тогда  ∠XCY= 30°.  Но и  ∠XYC= 30° (как внешний угол треугольникаCYB), следовательно, треугольникCXY– равнобедренный.   ПосколькуXM– биссектриса равнобедренного треугольникаCXY, то она также является медианой и высотой, следовательно,CMY– также равнобедренный, откуда  ∠MYC= ∠MCY= α.  С другой стороны,  ∠MBC= α,  то есть четырёхугольникCMYB– вписанный. Тогда  ∠MBY= ∠MCY= α,  откуда  2α = 15°,  α = 7,5°  и  ∠CMB= 150°.   Докажем, что точка X лежит на отрезке AM. Пусть это не так (см. рис.).   Снова рассмотрим треугольник AXB отдельно и проведем отрезок CY так, что  ∠YCB = 15°.  По условию,  ∠MCB = 15° + ∠MBC.  Так как

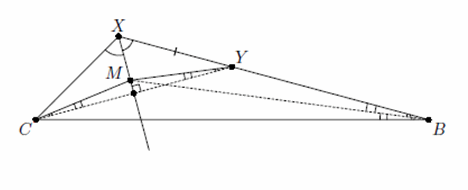
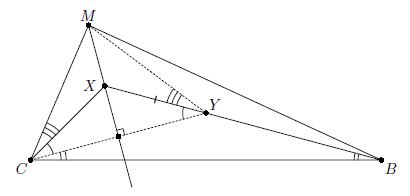
∠XCB = 30° + ∠XBC,  то чтобы выполнялось условие, угол MBX должен быть на 15° больше угла MCX. Треугольник CMY – равнобедренный, следовательно,  ∠MCX = ∠MYX > ∠MBY,  то есть такое расположение точек невозможно.

150°.