Задача
Биссектрисы AA1 и CC1 треугольника ABC пересекаются в точке I. Описанные окружности треугольников AIC1 и CIA1 повторно пересекают дуги AC и BC (не содержащие точек B и A соответственно) описанной окружности треугольника ABC в точках C2 и A2 соответственно. Докажите, что прямые A1A2 и C1C2 пересекаются на описанной окружности треугольника ABC.
Решение
Пусть X – точка пересечения прямой C1C2 и описанной окружности ω треугольника ABC (см. рис.).
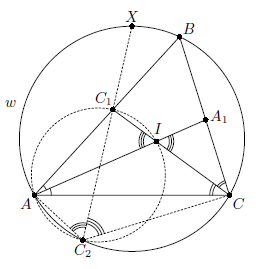
∠AC2C = 180° – ∠B, то ∠AC2X = ∠CC2X, то есть X – середина дуги AC.
То, что прямая A1A2 также пересекает ω в середине дуги ABC, доказывается аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет